PROPOSICIONES COMPUESTAS

Proposiciones compuestas (Disyunción, Conjunción, Negación, Condicional, Bicondicional)

 
de zector0k
DISYUNCIÓN
La disyunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.
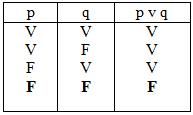
Tabla de verdad de la disyunción
Tabla de verdad de la disyunción
p v q (se lee: ” p o q”)
EJEMPLOS:
p = ” El numero 2 es par”
q = ” la suma de 2 + 2 es 4″
entonces…
pvq: “El numero 2 es par o la suma de 2 + 2 es 4″
p = ” La raíz cuadrada del 4 es 2”
q = ” El numero 3 es par″
entonces…
pvq: “La raíz cuadrada del 4 es 2 o el numero 3 es par”
CONJUNCIÓN
La conjunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderas.
Tabla de verdad de la conjunción
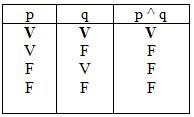
Tabla de verdad de la conjunción
 p ^ q (se lee: ” p y q”)
EJEMPLOS:
p = ” El numero 4 es par”
q = ”Siempre el residuo de los números pares es 2″
entonces…
p^q: “El numero 4 es par y Siempre el residuo de los números pares es 2″
p = ” El numero mas grande es el 34”
q = ”El triangulo tiene 3 lados″
entonces…
p^q: “El numero mas grande es el 34 y El triangulo tiene 3 lados”
NEGACIÓN
La negación es un operador que se ejecuta. sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.
Tabla de verdad de Negación
Tabla de verdad de Negación
EJEMPLOS
p:  “4 + 4 es igual a 9”
-p: “4 + 4 no es igual a 9″
p:  “El 4 es un numero par”
-p: “El 4 no es un numero par”
CONDICIONAL
El condicional material es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad falso sólo cuando la primera proposición es verdadera y la segunda falsa, yverdadero en cualquier otro caso.
La condicional de dos proposiciones p, q da lugar a la proposición; si p entonces q, se representa por p → q
Tabla de Verdad Condicional
Tabla de Verdad Condicional
EJEMPLOS
p:  “llueve”
q: “hay nubes”
p→q: “si llueve entonces hay nubes”
p:  “Hoy es miércoles”
q: “Mañana será jueves”
p→q: “Si Hoy es miércoles entonces Mañana será jueves”
BICONDICIONAL
El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad difieren.
Tabla de Verdad Bicondicional
Tabla de Verdad Bicondicional
EJEMPLOS
p:  “10 es un número impar”
q: “6 es un número primo”
p↔q: “10 es un número impar si y solo si 6 es un número primo”
p:  “3 + 2 = 7”
q: “4 + 4 = 8”
p↔q: “3 + 2 = 7  si y solo si 4 + 4 = 8″
https://www.blogger.com/blogger.g?blogID=7586512511876541706#editor/target=post;postID=3321858223301664319https://www.blogger.com/blogger.g?blogID=7586512511876541706#editor/target=post;postID=3321858223301664319

Comentarios

Publicar un comentario

Entradas populares de este blog

PLANIFICACION DE UNIDAD

Titulo de la unidad de aprendizaje Factorización Asignatura Matemática Tiempo Un mes Situación de aprendizaje Un estudiante   del Liceo Dr. José Francisco Peña Gómez observa una familia integrada por tres miembros padre, madre e hijo, y comprendió que entre el padre   y la madre hay un factor común que es su hijo. Competencias Fundamentales Ética y ciudadana, resolución de problemas, ambiental y de la salud, científica y tecnológica, desarrollo personal y espiritual Competencias Especificas Contenidos Conceptuales Procedimentales Actitudinales       Razona y argumenta         Clasifica polinomios según su número de términos y su grado.           E     Emplea definiciones, reglas, algoritmos en la resolución ...
Leer más

LA CIRCUNFERENCIA Y SUS ELEMENTOS

Imagen
  La circunferencia Definición:  La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elementos de la circunferencia. En una circunferencia podemos distinguir los siguientes elementos: Centro : es el punto situado en su interior que se encuentra a la misma distancia de cualquier punto de la circunferencia. Radio : es el segmento que une cualquier punto de la circunferencia con el centro. Cuerda : es el segmento que une dos puntos cualesquiera de la circunferencia. Diámetro : es la cuerda que pasa por el centro de la circunferencia. Arco : es el segmento de circunferencia comprendido entre dos de sus puntos. Semicircunferencia : es el arco que abarca la mitad de la circunferencia. Ecuación de la circunferencia ( x − a ) 2 + ( y − b ) 2 = R 2 ( � − � ) 2 + ( � − � ) 2 = � 2 En esta página proporcionamos la ecuación de la circunferencia de centro (a, b) y radio R, (x-a)²+(y-b)² = R², y de los círculos con y sin borde. Tm...
Leer más

INTRODUCCION A LOS POLINOMIOS

Imagen
  ¿Qué son los polinomios? El álgebra es la rama de las matemáticas que estudia los polinomios y lo define como una  expresión algebraica  formado por la combinación de varios términos que están unidos entre sí mediante operaciones de  suma  o  resta . También se puede definir un polinomio como la suma de varios   monomios   no semejantes. La palabra polinomio proviene de las palabras griegas “poli” que significa muchos y “nomio” que quiere decir término, así que polinomio es “muchos términos”. Aunque un polinomio es una expresión algebraica, no todas las expresiones algebraicas son polinomios. Entonces, para que una expresión algebraica sea considerada como un polinomio debe cumplir con las siguientes características: Los exponentes de las variables deben ser  números positivos  no  negativos . No debe haber variables en el denominador de fracciones que aparezcan en algún término. Las variables no deben estar dentro de ra...
Leer más