LA CIRCUNFERENCIA Y SUS ELEMENTOS
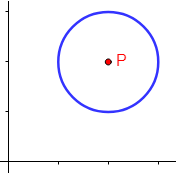
| La circunferencia Definición: La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. | |
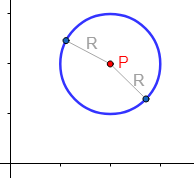
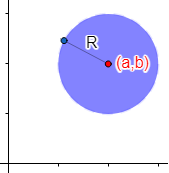
Elementos de la circunferencia.
Ecuación de la circunferenciaEn esta página proporcionamos la ecuación de la circunferencia de centro (a, b) y radio R, (x-a)²+(y-b)² = R², y de los círculos con y sin borde. Tmabién, resolvemos problemas resueltos relacionados, explicados paso a paso. Índice:
1. Definición de circunferenciaUna circunferencia en el plano se caracteriza por dos elementos: su centro y su radio. Dado un punto del plano, la circunferencia de centro y radio es el conjunto de puntos situados a una distancia de :
La distancia de cualquier punto de la circunferencia a su centro es exactamente :
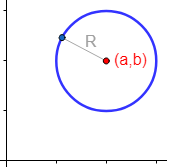
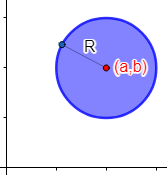
2. Ecuación de la circunferenciaLa ecuación de la circunferencia de centro y radio es
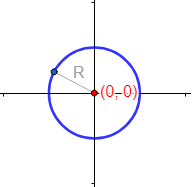
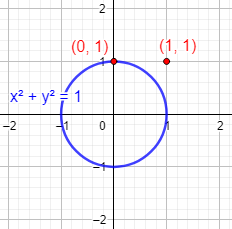
Si el centro es el origen de coordenadas , la ecuación es más sencilla:
3. Ecuación del círculoUn círculo es como una circunferencia, pero incluye su interior: Dado un punto del plano, el círculo de centro y radio es el conjunto de puntos situados a una distancia menor o igual que de . Por tanto, sólo tenemos que cambiar el signo por el signo en la ecuación de la circunferencia:
Finalmente, si no queremos el borde del círculo, escribimos el signo de desigualdad estricta:
4. Puntos de la circunferenciaSi queremos saber si un punto forma parte de una circunferencia dada (o de un círculo), sólo tenemos que comprobar si sus coordenadas cumplen la ecuación. EjemploComprobamos si el punto forma parte de la circunferencia :
Como el punto verifica la ecuación, está en la circunferencia. Veamos que el punto no está en la circunferencia:
Representación:
FUENTE: https://www.problemasyecuaciones.com/ |

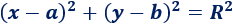
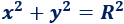
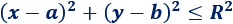
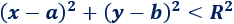
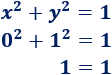
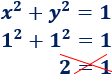
Comentarios
Publicar un comentario