PROPIEDADES GENERALES DE LOS LOGARITMOS

Propiedades de los logaritmos y ejemplos

Propiedad 1

El logaritmo en cualquier base de 1 es igual a 0:

Directamente, cuando veamos el logaritmo de 1, da igual la base que tenga, podemos sustituirla por un 0.

Por ejemplo:

Propiedad 2

Cuando en el logaritmo de un número, la base y el número son iguales, el resultado del logaritmo es 1:

Gracias a esta propiedad, podemos sustituir directamente un logaritmo con igual base e igual número por 1, si nos conviene para resolver ecuaciones:

Por ejemplo:

Propiedad 3

Cuando en el logaritmo de un número, la base y el número son iguales y el número está elevado a un exponente, el logaritmo será igual al exponente del número:

Esta propiedad es muy útil para convertir cualquier número en un logaritmo

Por ejemplo:

Con esta propiedad, también podemos calcular el valor de un logaritmo si es posible expresar el contenido del logaritmo como potencia de la misma base del logaritmo, como por ejemplo:

Escribimos el 81 en forma de potencias de 3:

Y directamente aplicando esta propiedad, vemos que el resultado es igual a 4.

Propiedad 4

El logaritmo en una base cualquiera de la multiplicación de dos números es igual a la suma de los logaritmos en esa misma base:

Por ejemplo para resolver un logaritmo de dos números multiplicándose:

Aplicamos la propiedad de la multiplicación:

Expresamos los números en forma de potencia:

Y aplicamos la propiedad 3 para resolver cada logaritmos y dar el resultado final:

Esta propiedad es una de la más utilizadas en la resolución de ecuaciones logarítmicas, ya que nos permite simplificar varios logaritmos en uno:

Propiedad 5

El logaritmo en una base cualquiera de la división de dos números es igual a la resta de los logaritmos en esa misma base:

Por ejemplo:

Aplicamos la propiedad de la división:

Expresamos los números en forma de potencia:

Y resolvemos los logaritmos aplicando la propiedad 3, ya que la base del logaritmo y la base de la potencia son iguales, llegando al resultado de la operación:

Junto con la propiedad anterior, permite simplificar varios logaritmos en uno sólo cuando estamos resolviendo ecuaciones logarítmicas:

Propiedad 6

Si tenemos un exponente en el logaritmo, ese exponente puede pasar a multiplicar al logaritmo:

Gracias a esta propiedad, podemos poner multiplicando el exponente, o colocar un número que multiplica al logaritmo como exponente según nos convenga.

Por ejemplo:

Aplicamos la propiedad poniendo el 6 multiplicando al logaritmo:

Ahora resolvemos el logaritmo sin el exponente, pasando el 512 a forma de potencia:

Calculamos el logaritmo aplicando la propiedad 3 y al final, multiplicamos los dos números que nos quedan:

Con esta propiedad, también podemos resolver los logaritmos de una raíz, como por ejemplo:

Ponemos la raíz en forma de potencia:

Y ahora el exponente lo colocamos delante del logaritmo multiplicando:

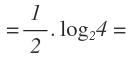
Ahora pasamos a resolver el logaritmo ya sin raíz. Ponemos el 4 en forma de potencia:

Resolvemos el logaritmo y lo multiplicamos por la fracción que teníamos delante:

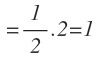
Para resolver ecuaciones logarítmicas, conviene deshacernos de los números que están multiplicando a los logaritmos. Esta propiedad, nos permite hacerlo, pasando el número como exponente del logaritmo, como por ejemplo:

Estas propiedades, son válidas para los logaritmos en cualquier base, por tanto, también se aplican para los logaritmos neperianos.

Aunque las propiedades de los logaritmos sean algo complejas de asimilar de forma aislada, cobran un mayor sentido cuando las apliquemos en la resolución de ecuaciones logarítmicas. Te lo explico más despacio en el Curso de Logaritmos.

https://www.blogger.com/blogger.g?blogID=7586512511876541706#editor/target=post;postID=3555683017335666882https://www.blogger.com/blogger.g?blogID=7586512511876541706#editor/target=post;postID=3555683017335666882