PROPIEDADES DE LA POTENCIACION
FACTORES: Cada una de las cantidades o expresiones que se multiplican para formar un producto.
LA POTENCIACION
La potenciación es una expresión matemática que incluye dos términos denominados: base a y exponente n.
Se escribe an, y se lee: «a elevado a n». Su definición varía según el conjunto numérico al que pertenezca el exponente:
Se escribe an, y se lee: «a elevado a n». Su definición varía según el conjunto numérico al que pertenezca el exponente:
- Cuando el exponente es un número natural, equivale a multiplicar un número por sí mismo varias veces: el exponente determina la cantidad de veces.
Por ejemplo:  .
.
 .
.
PROPIEDADES DE LA POTENCIACION
POTENCIA DE EXPONENTE 0
Un número (distinto de 0) elevado al exponente 0 da como resultado la unidad (1), puesto que:
POTENCIA DE EXPONENTE 1
Toda potencia de exponente 1 es igual a la base:TO
POTENCIA DE EXPONENTE NEGATIVO
Un número elevado a un exponente negativo, es igual al inverso de la misma expresión pero con exponente positivo:MULTIPLICACIÓN DE POTENCIAS DE IGUAL BASE
El producto de dos o más potencias de igual base es igual a la base elevada a la suma de los correspondientes exponentes (se escribe la misma base y se suman los exponentes):DIVISIÓN DE POTENCIAS DE IGUAL BASE
La división de dos potencias de igual base es igual a la base elevada a la resta de los exponentes respectivos:POTENCIA DE UN PRODUCTO
La potencia de un producto es igual al producto de los factores elevados cada uno al exponente de dicha potencia. Es decir, una potencia de base a.b y de exponente n, es igual al factor a elevado a n, multiplicado por el factor b también elevado a n:POTENCIA DE UNA POTENCIA
La potencia de una potencia de base a es igual a la potencia de base a y cuyo exponente es el producto de ambos exponentes (la misma base y se multiplican los exponentes): se reserva para significar
se reserva para significar 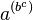 ya que
ya que  se puede escribir sencillamente como
se puede escribir sencillamente como  .Propiedad distributiva
.Propiedad distributivaLa potenciación es distributiva con respecto a la multiplicación y a la división:
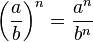


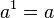

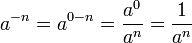



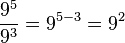
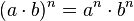
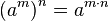
Comentarios
Publicar un comentario